5.1 Definición de transformación lineal

 Definición de transformación lineal 

En primer lugar, una transformación lineal es una función. Por ser función, tiene su dominio y su codo minio, con la particularidad de que éstos son espacios vectoriales. Tenemos dos espacios vectoriales $V$ y $W$, y una función que va de $V$ a $W$. O sea una regla de asignación que transforma vectores de $V$ en vectores de $W$. Pero no toda función que transforme vectores de $V$ en vectores de $W$ es una transformación lineal. Debe cumplir ciertas condiciones:

$F:V\to W$ es una transformación lineal si y sólo si:

1. $F\left(u+v\right)=F\left(u\right)+F\left(v\right)\forall u,v\in V$
2. $F\left(k.v\right)=k.F\left(v\right)\forall v\in V,\forall k\in$

Propiedades de transformación lineal

Propiedad 1

La imagen del vector nulo del dominio $0_V$ es el vector nulo del codo minio $0_w$:

$$T\left(0_V\right)=0_w$$

Demostración:

$$T\left(0_V\right)=T\left(0.v\right)=0.T\left(v\right)=0.w=0_W$$

Donde hemos expresado a $0_V$ como el producto del escalar $0$ por cualquier vector del espacio vectorial $V$, hemos usado la segunda condición que debe cumplir una transformación lineal, y finalmente hemos vuelto a usar la propiedad de espacios vectoriales sobre el producto del escalar 0 por cualquier vector.

Propiedad 2

La imagen del vector $–v$ es igual al opuesto de la imagen de $v$:

$$T\left(–v\right)=–T\left(v\right)$$

Demostración:

$$T\left(–v\right)=T\left(–1.v\right)=–1.T\left(v\right)=–T\left(v\right)$$

La justificación de los pasos dados en la demostración es similar a la anterior.

Propiedad 3

Consideremos $r$ vectores del espacio vectorial $V$:

$$v_1,v_2,\dots ,v_r\in V$$

Tomemos una combinación lineal en el dominio:

$${\alpha }_1{v}_1+{\alpha }_2{v}_2+{\alpha }_3{v}_3+...+{\alpha }_r{v}_r$$

Donde ${\alpha }_i\in R$.

Si aplicamos la transformación lineal $F$ de $V$ a $W$, teniendo en cuenta las propiedades enunciadas en la definición, resulta:

$$F\left({\alpha }_1{v}_1+{\alpha }_2{v}_2+{\alpha }_3{v}_3+...+{\alpha }_r{v}_r\right)={\alpha }_{1}F\left(v_1\right)+{\alpha }_{2}F\left(v_2\right)+\dots +{\alpha }_{r}F\left(v_r\right)$$

Es decir que una transformación lineal «transporta» combinaciones lineales de $V$ a $W$, conservando los escalares de la combinación lineal.

Ejemplo 1

Analizar si la siguiente función es una transformación lineal:

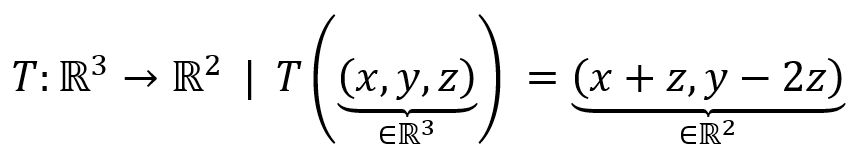
Resolución

Controlemos primero que el transformado del $0_V$ sea el $0_W$. Ésta es una condición necesaria: si no se cumpliera, no sería transformación lineal. Como $T\left(\left(0,0,0\right)\right)=\left(0,0\right)$, la función dada es «candidata» a ser transformación lineal. Para demostrar que es una transformación lineal tenemos que comprobar las condiciones dadas en la definición.

Condición 1: $T\left(u+v\right)=T\left(u\right)+T\left(v\right)\forall u,v\in V$

Tomemos dos vectores de $R^3$

$$u=\left(u_1,u_2,u_3\right)$$

$$v=\left(v_1,v_2,v_3\right)$$

Veamos si

$$T\left(u+v\right)=T\left(u\right)+T\left(v\right)$$

Primero hacemos la suma de $u$ y $v$:

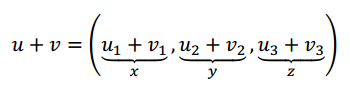
Y ahora aplicamos $T$:

$$T\left(u+v\right)=\left(u_1+v_1+u_3+v_3,u_2+v_2–2u_3–2v_3\right)$$

$$T\left(u+v\right)=T\left(u\right)+T\left(v\right)$$

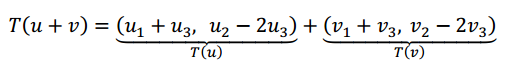
En conclusión: se cumple la primera de las condiciones.

Nos faltaría la otra propiedad.

Condición 2: $T\left(k.v\right)=k.T\left(v\right)\forall v\in V,\forall k\in R$

$$T\left(k.v\right)=T\left(\left(k{v}_1,k{v}_2,k{v}_3\right)\right)=\left(k{v}_1+k{v}_3,k{v}_2–2k{v}_3\right)$$

$$=k.\left(v_1+v_3,v_2–2v_3\right)=k.T\left(v\right)$$

Como $T$ cumple las dos condiciones, es una transformación lineal.

Un video para que quede mas claro el tema